Sandrine Dallaporta, l’aléatoire derrière nos films

Sandrine Dallaporta est née et a grandi à Toulouse, au sud de la France. Elle raconte ce qui l’a poussée à choisir la recherche scientifique où elle s’épanouit grâce aux mathématiques.

L’intérêt pour les mathématiques de Sandrine Dallaporta est né dans son enfance. Au contact de son professeur de mathématiques au lycée, cet intérêt a mûri. Encouragée par ses bons résultats dans les matières scientifiques et en particulier en mathématiques, c’est tout naturellement qu’elle poursuit ses études en classes préparatoires mathématiques-physique au lycée Pierre de Fermat à Toulouse. En effet, très attirée par la pluridisciplinarité de ce cursus, son objectif professionnel n’étant pas encore clairement établi, cette option lui semble être la meilleure. À l’issue de ces deux ans, elle choisit de devenir enseignante-chercheuse. Dans cette optique, elle décide d’intégrer l’École normale supérieure de Lyon. Après avoir effectué trois ans dans cet établissement, elle a l’opportunité d’effectuer sa deuxième année d’ENS à l’université de Montréal. Elle poursuit ses études en Master 2 (spécialité : Probabilités et statistiques) à l’université de Toulouse. Enfin, elle obtient son agrégation en 2008.

Elle commence sa thèse intitulée «Quelques aspects de l’étude quantitative de la fonction de comptage et des valeurs propres de matrices aléatoires» à l’université de Toulouse sous la direction de Michel Ledoux.

Après sa thèse, elle continue son parcours dans le monde de la recherche. Elle obtient un poste à l’université Paris-Saclay comme enseignante-chercheuse (agrégée préparatrice). Ce poste est contractuel et elle y restera sept ans. En septembre 2019, Sandrine Dallaporta obtient un poste de maître de conférences à l’université de Poitiers. Elle intègre l’équipe de Probabilités et statistiques au laboratoire de mathématiques et applications (LMA). Sa thématique de recherche est la théorie des matrices aléatoires. 

Mais que se cache-t-il derrière cet étrange intitulé ? Les matrices aléatoires sont introduites dans les années 1920 par le statisticien Wishart afin de répondre à des problèmes apparaissant lorsque l’on utilise des données de très grandes dimensions, voire infinies. Depuis elles ont été au centre des intérêts de différents mathématiciens ou physiciens. Particulièrement, Wigner en 1950, qui révolutionne la compréhension de la physique nucléaire grâce aux matrices aléatoires. Depuis lors, la théorie des matrices aléatoires a trouvé de très nombreuses applications. On les retrouve, par exemple, en statistiques, dans la finance, en télécommunication, dans les graphes aléatoires, dans la combinatoire, dans les systèmes intégrables, en traitement du signal, ou encore dans le chaos quantique.

Un problème connu est celui de Netflix, dont une grande récompense a été décernée pour sa résolution à l’aide des matrices aléatoires. Le problème est le suivant : une très grande matrice est faite à partir des utilisateurs, des films et des séries. Leurs intersections sont les notes que mettent les utilisateurs aux contenus. La matrice dispose de très peu de points connus : seules les notes données par les utilisateurs sont renseignées. Les points inconnus sont toutes les absences de notes pour un film (ou série) par un utilisateur. Netflix souhaiterait recommander ou non des films aux utilisateurs. La récompense sera remportée par la personne qui remplira la matrice avec le moins d’erreurs possible (c’est-à-dire les meilleures recommandations). Le problème a été résolu à l’aide des matrices aléatoires. Ce fut le début du compressed sensing ou compressive sensing.

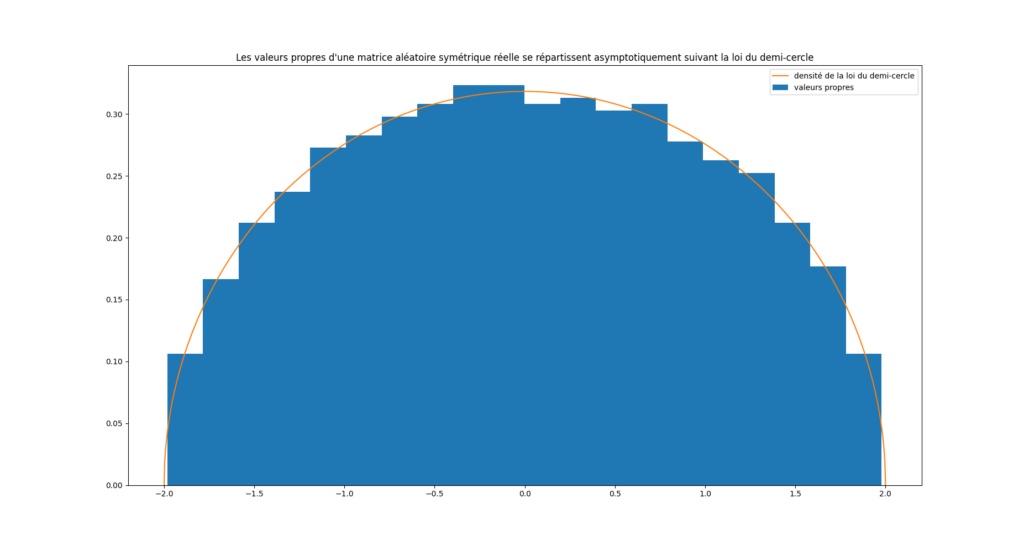
Ce sujet a inspiré Sandrine Dallaporta durant sa thèse où elle s’est intéressée aux propriétés de matrices à tailles fixées au travers notamment du nombre de valeurs propres présentes dans un intervalle. Elle étudie ce domaine des mathématiques de façon théorique plus que numérique et elle y contribue en étudiant les valeurs propres et leur vitesse de convergence.

«Le monde n’est ni joyeux ni cruel. Il est simplement aléatoire.»
Harlan Coben