Géométrie algorithmique et monde réel
 Modélisation 3D de Beethoven (à gauche) et d’un galion (à droite) par maillage. Pierre Alliez, Craig Gotsman. Recent Advances in Compression of 3D Meshes, Inria, 2003.
Modélisation 3D de Beethoven (à gauche) et d’un galion (à droite) par maillage. Pierre Alliez, Craig Gotsman. Recent Advances in Compression of 3D Meshes, Inria, 2003.Par Rachad Bentbib, Rémy Bouché, Simone Novario.
La géométrie algorithmique trouve ses origines dans les années 1960 avec la naissance de la conception assistée par ordinateur (CAO). Le monde industriel souhaite exploiter les outils informatiques pour se passer des innombrables maquettes et plans utilisés en conception.
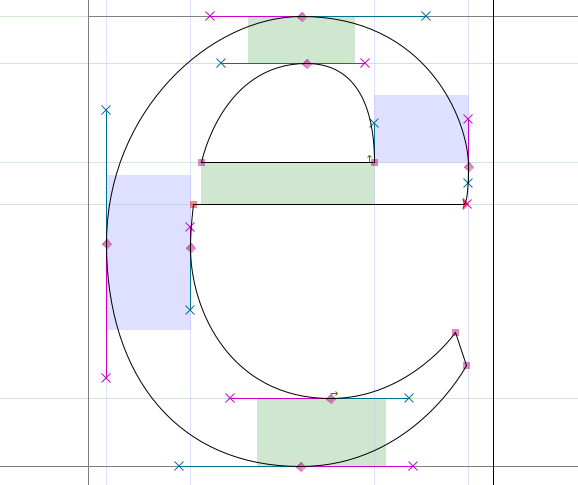
Paul de Casteljau, mathématicien français, développe une méthode pour approximer des surfaces par des courbes polynomiales pour la société Citroën. Quatre années plus tard, Pierre Bézier travaille sur la représentation informatique de ces courbes pour Renault. Ces courbes, connues sous le nom de courbes de Bézier, trouvent aujourd’hui de nombreuses applications dans la synthèse d’images en informatique.
Une autre date clé de l’histoire de la géométrie algorithmique est 1978, avec la thèse de Michael Shanos, intitulée Computational Geometry (Géométrie algorithmique). Shanos met en place des outils et techniques mathématiques pour la résolution de problèmes géométriques à l’aide d’un ordinateur. Bien que son travail n’ait pas permis d’obtenir directement des solutions concrètes à la modélisation des objets en trois dimensions, il a joué un rôle fondamental en posant les bases de cette nouvelle discipline. Sa thèse présente des résolutions de nombreux problèmes de manière innovante et efficace, ainsi que des algorithmes plus performants réduisant le temps de calcul.
La modélisation 3D connaît une avancée décisive avec l’apparition de la numérisation de formes. Au début des années 1980, le laboratoire Inria développe un premier capteur de numérisation : l’appareil scanne la forme à l’aide d’un système Laser en déterminant la position de plusieurs points par triangulation. Pour la première fois, il est possible de sauvegarder une forme tridimensionnelle de manière simple et précise. L’instrumentation a évolué. Maintenant accessible au grand public, elle est présente dans de nombreuses applications : cartographie, cinéma, jeux vidéo, architecture, etc.
La numérisation 3D et le maillage
Une fois les bases de la géométrie algorithmique établies, les mathématiciens se sont intéressés à une question fondamentale : Comment représenter les formes géométriques, continues, par des modèles discrets ?
Pour notre cerveau, ce passage se fait naturellement puisque nous avons tendance à distinguer et interpréter des formes à partir d’un ensemble de points, pour peu que leur densité soit suffisante. Boissonnat prend l’exemple du mouvement artistique pointilliste, consistant à peindre par petites touches de couleurs juxtaposées.

Le pointillisme est un exemple de passage du discret au continu que nous opérons au quotidien.
En revanche, cette approximation est impossible en mathématiques. Le passage du discret au continu a occupé une grande place dans le domaine du traitement du signal et des images, avec notamment les travaux de Claude Shannon sur le sujet dans les années 1960. Dans le domaine de la géométrie, cette question s’est posée plus tardivement. Herbert Federer, un mathématicien américain, introduit en 1969 la notion de «portée», qui a pour but de résumer en un nombre la complexité d’une forme géométrique. Plus la complexité de la forme est élevée plus la résolution doit être fine, c’est-à-dire qu’elle doit présenter un nombre de points important pour être modélisée correctement.
La reconstruction de forme tridimensionnelle à partir d’un ensemble de points discrets est réalisée lors de l’étape de maillage. À l’issue de cette phase, les points sont reliés en une multitude de facettes pour construire des surfaces, et en polyèdres pour constituer des volumes. Les mathématiciens se basent sur trois critères pour définir la qualité du maillage construit :
- la distance entre les points ;
- l’angle entre les facettes et la surface ;
- la conservation de la topologie.
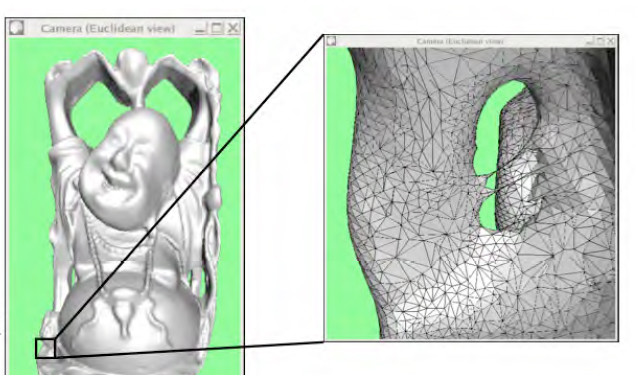
La méthode la plus efficace pour respecter ces critères est la triangulation de Delaunay restreinte. Les modèles construits à partir de cette technique sont constitués de facettes triangulaires et de tétraèdres. De nos jours, avec les progrès de l’informatique, il est courant de travailler avec des maillages dépassant le million de tétraèdres.
Difficultés numériques
Si les techniques développées sont pertinentes en théorie, beaucoup de difficultés peuvent être rencontrées dans leur mise en pratique, en particulier dans le cadre des grandes dimensions.
En effet, lorsqu’on monte en dimension le coût de la représentation géométrique des données croît de manière exponentielle. Le coût du stockage et le temps nécessaire pour les calculs croissent de la même manière. Pour mieux appréhender ce que d’aucuns appellent le fléau de la dimension, imaginez un espace 2D échantillonné avec une résolution de un millième, par une grille de 1000 par 1000, soit un million de carrés. Un espace 3D échantillonné avec la même résolution par une grille cubique contient, quant à lui un milliard de cubes. Les données, dont la géométrie décrit une surface qui ne peut être représentée qu’en dimension bien supérieure, introduit beaucoup de complexité. Ceci augmente énormément le coût en espace de stockage et en temps nécessaire pour que l’ordinateur fasse des calculs.
Boissonnat prend l’exemple de l’étude du paysage énergétique des molécules. Une molécule possède plusieurs formes différentes dues aux rotations des atomes constituant la molécule, qu’on appelle conformères. Un conformère d’une molécule à n atomes peut être décrit par 3n nombres correspondants aux 3 coordonnées de chaque atome, et ainsi un conformère peut être vu comme un point dans un espace de dimension 3n.
Dans le cas de la molécule de cyclooctane C8H16, il y a 24 atomes, donc les différentes conformations sont décrites dans un espace de dimension 72. Cependant, l’ensemble de ses conformères décrit une union d’une sphère et d’une bouteille de Klein, deux surfaces de dimension 2, et le tout ne demande que 5 dimensions pour être représenté.
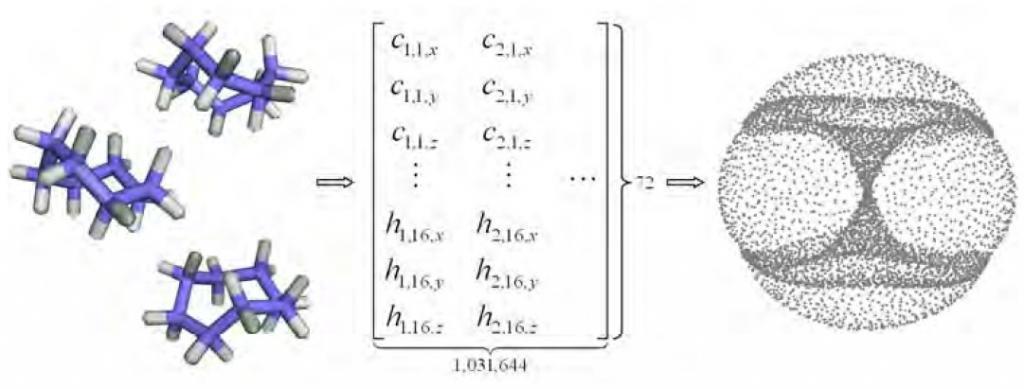
Martin, Shawn, et al. “Topology of cyclo-octane energy landscape.” The journal of chemical physics 132.23 (2010)
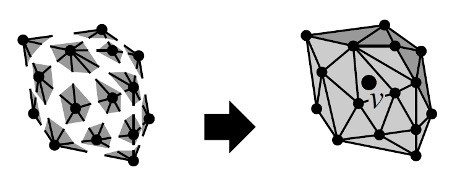
Pour éviter de travailler dans des dimensions très grandes, Boissonnat, ainsi que d’autres chercheurs, ont développé des algorithmes de triangulations de telles surfaces de dimension 2 sans se préoccuper de la dimension de l’espace ambiant. L’idée est d’utiliser le fait que de telles surfaces sont des unions de variétés de dimension 2, c’est-à-dire des surfaces qu’on perçoit comme différents recollements particuliers de morceaux de plans représentants différentes régions de la surface, tel un atlas, et cela sans se soucier de l’espace ambiant.
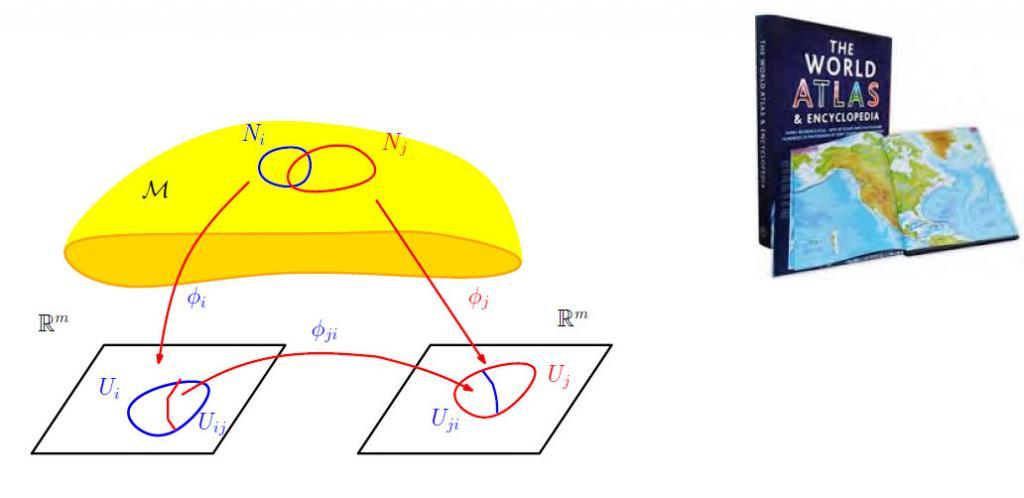
comme sur l’image à gauche.
L’algorithme calcule des triangulations locales en chaque morceau qui est de dimension 2, puis les recolle (voir figure ci-dessous).
Jean-Daniel Boissonnat, directeur de recherche au laboratoire INRIA de l’université de Sophia-Antipolis, présente ses travaux dans une conférence au Collège de France intitulée «Géométrie algorithmique : des données géométriques à la géométrie des données». Ce domaine s’intéresse à la représentation efficace des formes géométriques sur ordinateurs et aux algorithmes travaillant efficacement sur ces représentations.
Cet article est écrit à partir de la conférence au Collège de France : Géométrie algorithmique : des données géométriques à la géométrie des données, donnée le 23 mars 2017.
Jean-Daniel Boissonnat, Dyer Ramsay, Ghosh Arijit, “Delaunay triangulation of manifolds.” Foundations of Computational Mathematics 18.2, 2018.
Cet article a été réalisé dans le cadre d’une formation à l’écriture journalistique avec l’École doctorale Sciences et ingénierie des systèmes, mathématiques, informatiques (Sismi) des universités de Poitiers et Limoges.
Auteurs
Rémy Bouché est doctorant en radiofréquences, Laboratoire XLIM, université de Limoges, sujet de thèse : «Conception hybride de fonctions hyperfréquences et numériques en technologie SiGe pour antenne à balayage électronique en bande Ka destinée aux télécommunications satellitaires».
Simone Novario est doctorant en mathématiques, Laboratoire LMA, université de Poitiers, sujet de thèse : «Systèmes linéaires sur les variétés symplectiques holomorphes irréductibles».
Rachad Bentbib est doctorant en mathématiques, université de Poitiers, laboratoire LMA (Laboratoire Mathématiques et Applications). Sujet de thèse : «Groupes en théorie des modèles, conjecture de Cherlin-Zilber : mauvais groupes et autres groupes pathologiques de rang de Morley fini» sous la direction de Olivier Frécon.

 Espace Mendès France
Espace Mendès France
Leave a comment